|
|
| 数理工学研究室/研究紹介 |
久保田研究室で行っている主な研究テーマは,
1.脳の数理モデル(計算論的神経科学・深層学習)
2.有機太陽電池の光制御技術
です.どちらの研究でもプログラミング言語(C/C++, MATLAB等)を習得した上で,数理モデルの解析を行います.数値シミュレーションにより複雑な現象を計算機上で再現することで,現象の本質を見抜くとともに全体像(big
picture)を描くことができます.(研究室紹介動画)
1.脳の数理モデル(計算論的神経科学・深層学習)
脳の優れた情報処理の仕組みを解明するために,様々な分野から実験・臨床研究が行われて膨大なデータが蓄積しています.しかし,脳の情報処理を司る神経細胞・神経ネットワークの多様かつ複雑な振る舞いが,現象の本質的な理解を阻んでいます.このため,実験データに潜む数理的な構造や特徴を明らかにする数理工学の役割がますます重要になっています.
久保田研では,神経の電気的活動を計算機上で再現する神経回路シミュレーションにより,神経現象を様々な角度から解析・予測することで包括的な理解を目指します.この研究では,子供の脳で見られる神経回路形成の仕組みや脳の病気(パーキンソン病等)のメカニズムの解明,神経回路と遺伝子発現の相互作用といった幅広いテーマを扱います.
さらに,高度な脳機能のモデルとして深層学習(AI)の研究も行っています.深層学習の研究では,学生の独自のアイデア・発想に基づいてテーマを決めています.これまでの本研究室の学生は,
・立体的に積まれた積み木の数の推定,安定性の判別
・部分的に隠した物体の写真によるクラス分類
・クロマキー合成を用いた背景画像の作成によるデータ拡張技術
・透明な容器に入れた液体の1方向からの画像による体積予測
・2つの三角形が相似/合同かどうか(幾何学的条件)の判定
といった,AIを応用した様々な興味深いテーマに取り組んでいます.画像認識が中心ですが,その他の学習モデルを研究する学生もいます.
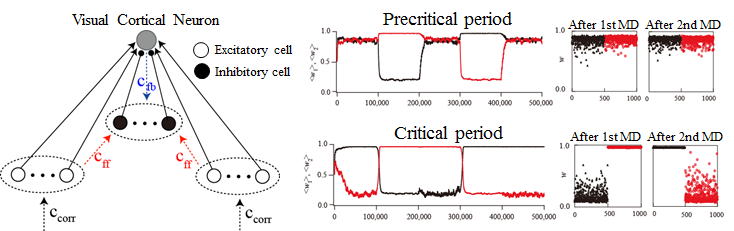
視覚野眼優位可塑性の臨界期のタイミングが,抑制性神経伝達(GABA)によって制御されることを示したモデル.左:両眼からのシナプス入力とフィードバック抑制を受ける視覚野神経細胞モデル.中・右:単眼遮蔽を受ける際の,両眼からのシナプス入力強度の変化.臨界期には,シナプス荷重の双安定なダイナミクスにより,感覚入力の履歴をシナプス荷重に埋め込むことができる.
I. Sakurai, S. Kubota, & M. Niwano, The onset and closure of critical
period plasticity regulated by feedforward inhibition, Neurocomputing 143, 261-268, 2014.
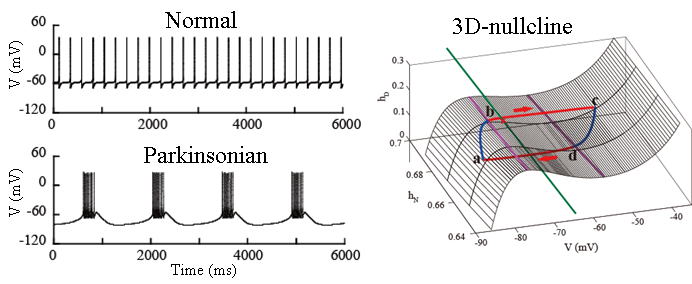
パーキンソン病に関連した大脳基底核のバースト振動のモデル.左:視床下核神経のコンパートメントモデルの膜電位応答.NMDA入力と過分極性電流が共存する時に,低周波数(<1
Hz)の強いバースト発火が誘発される.右:提案する3次元ヌルクライン法により,バースト発火が発生するための,非線形力学系としてのメカニズムを解析した例.
S. Kubota & J. Rubin, NMDA-induced burst firing in a model subthalamic
nucleus neuron, J Neurophysiol, 106, 527-537, 2011. (日本語論文はこちらから)
その他の研究例:
(1)NMDAR・GABAの遺伝子発現が皮質神経回路の組織化に及ぼす影響
S. Kubota & T. Kitajima, A model for synpatic development regulated
by NMDA receptor subunit expression, J Comput Neurosci 24, 1-20, 2008
I. Sakurai, S. Kubota, & M. Niwano, A model for ocular dominance plasticity
controlled by feedforward and feedback inhibition, IEICE E97-A, 1780-1786, 2014
(2)神経活動フィードバックを伴うスパイクタイミング依存シナプス可塑性(STDP)のモデル
S. Kubota, J. Rubin, & T. Kiajima, Modulation of LTP/LTD balance in
STDP by an activity-dependent feedback mechanism, Neural Networks 22, 527-535, 2009,
S. Kubota & T. Kitajima, Possible role of cooperative action of NMDA
receptor and GABA function in developmental plasticity, J Comput Neurosci 28, 347-359, 2010
S. Kubota, Activity-dependent competition regulated by nonlinear interspike
interaction in STDP: A model for visual cortical plasticity. Artif Life Robotics 17, 152-157, 2012
(3)神経場方程式の非線形解析
S. Kubota, K. Hamaguchi, & K. Aihara, Local excitation solutions in
one-dimensional neural fields by external input stimuli. Neural Comput & Appl 18, 591-602, 2009
(4)パーキンソン病に関連した神経回路モデル
S. Kubota & J. E. Rubin, Numerical optimization of coordinated reset
stimulation for desynchronizing neuronal network dynamics, J Comput Neurosci 45: 45-58, 2018.
2.有機太陽電池の光制御技術
太陽電池のコスト削減,フレキシブル化,軽量化を目指して,有機太陽電池の開発が近年活発に行われています.有機太陽電池の発電効率をさらに向上させるために,非常に薄い(100
nm程度.1 nm = 10-9 m)発電層に光を閉じこめることを可能にする,優れた光制御技術の開発が強く期待されています.
久保田研では,有機太陽電池の光学シミュレーションを用いて光の流れを最適に制御することで,発電効率を改良するための新しい光制御構造の開発を行っています.この研究では,数100 nmの高さを持つ極小な円錐を並べたモスアイ(蛾の眼)構造の最適設計を行い,実際に試作して太陽電池に適用することで高い発電性能を実現しています.このように自分で設計した太陽電池・反射防止構造を実際に製作することもできます.さらに,深層学習(AI)を応用した新しい発想の光制御構造の設計法の開発にも取り組んでいます.
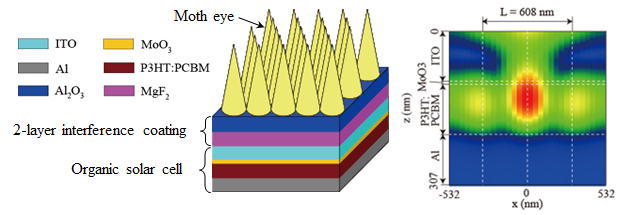
モスアイ構造(ナノテクスチャ)と多層干渉膜を組み合わせた有機太陽電池用ハイブリッド反射防止構造の最適設計.左:提案するハイブリッド反射防止構造と有機太陽電池の光学モデル.右:FDTD法のシミュレーションにより得られた太陽電池内部の電界分布.反射防止により,発電層のほぼ全領域で電界が強められて光吸収が促進されている.
S. Kubota, K. Kanomata, T. Suzuki, B. Ahmmad, & F. Hirose, Hybrid antireflection
structure with moth eye and multilayer coating for organic photovoltaics,
J Coat Technol Res, 12: 37-47, 2015.
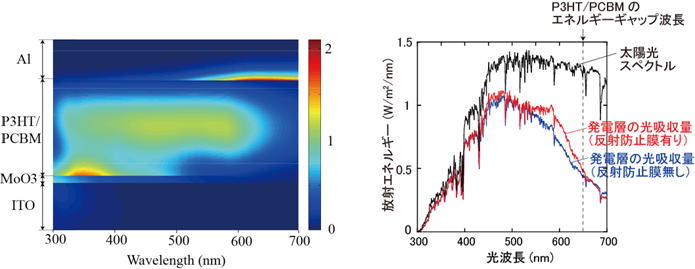
P3HT/PCBM型有機太陽電池内部の光吸収分布の解析例.左:多層干渉膜を導入した有機太陽電池内部の光吸収分布(特性マトリクス法のシミュレーションによる).右:反射防止膜を導入することで,主に長波長での発電層の吸収エネルギーの増加が起きる.
S. Kubota, K. Kanomata, K. Momiyama, T. Suzuki, & F. Hirose, Robust
design method of multilayer antireflection coating for organic solar cells,
IEICE, E96-C: 604-611, 2013. (日本語論文はこちらから)
その他の研究例:
(1)ガラス基板を光が通過するデバイスへのFDTD法の適用とモスアイ構造の最適化
S. Kubota, K. Kanomata, B. Ahmmad, J. Mizuno, & F. Hirose, Optimized
design of moth eye antireflection structure for organic photovoltaics,
J Coat Technol Res, 13: 201-210, 2016.
S. Kubota, K. Kanomata, B. Ahmmad, J. Mizuno, & F. Hirose, FDTD analysis
for light passing through glass substrate and its application to organic
photovoltaics with moth eye antireflection coating, J Photopolym Sci Technol, 29: 209-214, 2016.
S. Kubota, K. Hiraga, K. Kanomata, B. Ahmmad, J. Mizuno, and F. Hirose,
Efficient light trapping structures for organic photovoltaics fabricated
by nanoimprint lithography, J Photopolym Sci Technol, 33: 103-109, 2020.
(2)ナノテクスチャと高屈折率ガラスを統合した有機太陽電池デバイスの設計及び評価実験
S. Kubota, Y. Harada, T. Sudo, K. Kanomata, B. Ahmmad, J. Mizuno, &
F. Hirose, An integrated antireflection design using nanotexture and high-refractive-index
glass for organic photovoltaics, J Coat Technol Res, 14: 1209-1224, 2017.
(3)屋内太陽電池用の反射防止膜の設計法
S. Kubota, B. Ahmmad, and F. Hirose, Optical design of multilayer antireflection
coatings for indoor solar cell applications, Applied Optics, 62: 2117-2123, 2023.
(4)光閉じ込め技術に関する総説論文
久保田 繁, 有馬ボシールアハンマド, 廣瀬文彦, “表面ナノ構造を用いた有機薄膜太陽電池の光閉じ込め技術”, 電子情報通信学会論文誌C, J106-C:
267-276, 2023. (招待論文) |
|