|
|
Shigeru Kubota
Professor,
Graduate School of Science and Engineering, Yamagata University
4-3-16 Jonan, Yonezawa, Yamagata, 992-8510, Japan
Welcome to my homepage
This laboratory addresses the study of mathematical engineering, in which
a mathematical model (i.e., dynamical equations) for real-world phenomena
is developed and analyzed by using advanced numerical simulation. The use
of a mathematical model is beneficial to clarify the relationship among
various complex phenomena, showing a big picture of them. Main research
topics are (1) Mathematical modeling of the brain (Computational neuroscience) and (2) Light management for organic solar cells. For the study of solar cells (2), we also perform experiments of producing
actual solar cell devices to verify and realize the simulation results.
1. Mathematical modeling of the brain (Computational neuroscience)
My research interest in computational neuroscience includes broad areas,
such as the organization of synaptic circuits in the cortex, the bursting
oscillation in the basal ganglia, and the interaction between neuronal
activity and the gene expression of synaptic receptors. Recently, I have
examined biophysical mechchanisms by which the opening and closure of the
critical period of visual cortical plasticty can be regulated through the maturation of GABA inhibition (Sakurai, Kubota, Niwano, Neurocomputing, 2014). This study suggests that the activity-dependent competition between
the inputs from two eyes to a visual cortical cell may contorl the timing
of developmental plasticity. I have also proposed a model of activity-dependent feedback (ADFB) of spike-timing-dependent plasticity (STDP) (Kubota, Rubin, Kitajima, Neural Networks 2009; Kubota and Kitajima, J Comput Neurosci 2010). The ADFB function provides STDP with the ability for dynamically modulating
the balance in long-term plasticity (LTP) and long-term depression (LTD),
and additionally, the ability for the swithcing between the Hebbian and
anti-Hebbian plasticity regimes.
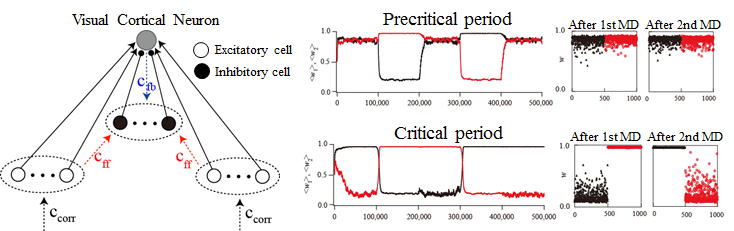
Numerical optimization of deep brain stimulation used for the treatment
of Parkinson's disease. By applying the spatially-distributed current stimuli
with the optimized waveform, synchronous network activity, which is a hallmark
of the disease, can be effectively prevented. (S. Kubota & J. E. Rubin, Numerical optimization of coordinated reset
stimulation for desynchronizing neuronal network dynamics, J Comput Neurosci 45: 45-58, 2018.)
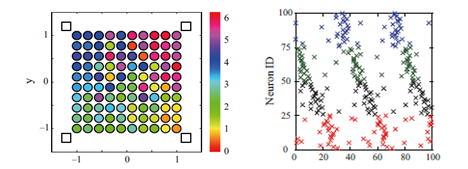
A model for explaining the mechanism of critical period plasticity in the
visual cortex. Left: A model cortical neuron receives afferent inputs from
both the left and right eyes. Right: synaptic weight dynamics in response
to monocular deprivation before and during the critical period (Sakurai, Kubota, & Niwano, The onset and closure of critical period
plasticity regulated by feedforward inhibition, Neurocomputing, 143, 261-268, 2014).
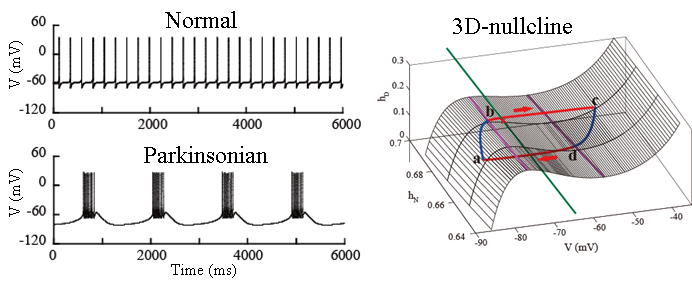
Bursting oscillation in the basal ganglia which is associated with Parkinson's disease. Left: examples of the time course of membrane potential of subthalamic nucleus neurons. Right: the 3-dimensional nullcline for analyzing the nonlinear dynamics of bursting activity (S. Kubota & J. Rubin, NMDA-induced burst firing in a model subthalamic
nucleus neuron, J Neurophysiol, 106, 527-537, 2011).
Examples of other studies:
(1)The effect of gene expression linked to NMDA receptor and GABA on the
synaptic organization
S. Kubota & T. Kitajima, A model for synpatic development regulated
by NMDA receptor subunit expression, J Comput Neurosci 24, 1-20, 2008
I. Sakurai, S. Kubota, & M. Niwano, A model for ocular dominance plasticity
controlled by feedforward and feedback inhibition, IEICE E97-A, 1780-1786, 2014
(2)Spike-timing-dependent plasticity (STDP) with activity-dependent feedback
(ADFB) mechanism
S. Kubota, J. Rubin, & T. Kiajima, Modulation of LTP/LTD balance in
STDP by an activity-dependent feedback mechanism, Neural Networks 22, 527-535, 2009,
S. Kubota & T. Kitajima, Possible role of cooperative action of NMDA
receptor and GABA function in developmental plasticity, J Comput Neurosci 28, 347-359, 2010
S. Kubota, Activity-dependent competition regulated by nonlinear interspike
interaction in STDP: A model for visual cortical plasticity. Artif Life Robotics 17, 152-157, 2012
(3)Nonlinear analysis of a neural field model
S. Kubota, K. Hamaguchi, & K. Aihara, Local excitation solutions in
one-dimensional neural fields by external input stimuli. Neural Comput & Appl 18, 591-602, 2009
2. Light management for organic solar cells
In the reserach of solar cell, I explore optimal structures of photovolitaic devices and their antireflection system (ARS) by using optical simulation. I am particularly interested in the
development of ARS for broadband light trapping of organic photovoltaics (OPVs). OPVs have been receiving high interest due to their potential for large-area, flexible, and low-cost solar cells. The power convergion efficacy (PCE) of OPVs has drastically increased in the past decade, although further increase will be required for large-scale commercialization. An important factor limiting the PCE of organic solar cells is low carrier mobility of organic semiconductors. To improve the carrier extraction from them, the thickness of active layer should be as thin as 100 nm. Therefore, it is quite important to develop efficient ARS by which sunlight can be trapped in such very thin active layer. To find optimal ARS, we combine various optimization techniques (e.g., multistart, quasi-Newton method, and pattern search) with simulations of Maxwell's equations using the chracteristic matrix method and finite-difference time-domain (FDTD) method (Kubota et al. J Coat Technol, 2014; Kubota et al. IEICE 2013).
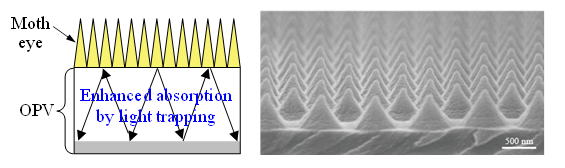 Application of moth eye surfaces, which is a periodic array of cones with
nanometer-order size, can significantly improve the efficiency of OPVs
by enhancing light trapping in the active layer. The geometry of moth eye
pattern, such as the height and period, is optimized through FDTD simulations.
Left: Schematic diagram for the light trapping effect. Right: SEM micrograph
of moth eye structure.(S. Kubota, K. Hiraga, K. Kanomata, B. Ahmmad, J. Mizuno, and F. Hirose,
Efficient light trapping structures for organic photovoltaics fabricated
by nanoimprint lithography, J Photopolym Sci Technol, 33: 103-109, 2020.) Application of moth eye surfaces, which is a periodic array of cones with
nanometer-order size, can significantly improve the efficiency of OPVs
by enhancing light trapping in the active layer. The geometry of moth eye
pattern, such as the height and period, is optimized through FDTD simulations.
Left: Schematic diagram for the light trapping effect. Right: SEM micrograph
of moth eye structure.(S. Kubota, K. Hiraga, K. Kanomata, B. Ahmmad, J. Mizuno, and F. Hirose,
Efficient light trapping structures for organic photovoltaics fabricated
by nanoimprint lithography, J Photopolym Sci Technol, 33: 103-109, 2020.)
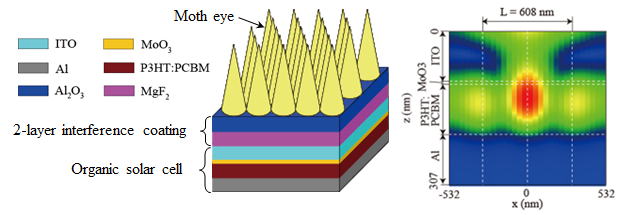
Hybrid antireflection structure for organic photovoltaics. Left: the layer
configuration of the solar cell device incorporated with the proposed hybrid
antireflecition sytem. Right: the spatial distribution of electric field
intensity within the solar cell, which is obtained by the FDTD simulation
(Kubota, Kanoamata, Suzuki, Ahmmad, & Hirose, Hybrid antireflection
structure with moth eye and multilayer coating for organic photovoltaics,
J Coat Technol, 12: 37-47, 2015).
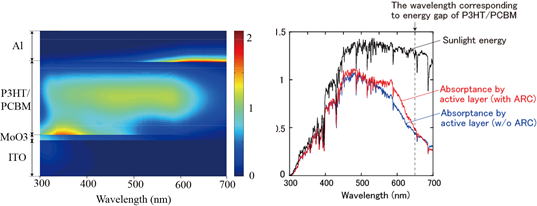
Optical analysis of P3HT/PCBM-based solar cell. Left: the spacial and spectral
distribution of absorbance within the solar cell is shown by the background
color. Right: The change in the absorbed energy spectrum by the optimized
multilayer antireflection structure (S. Kubota, K. Kanomata, K. Momiyama, T. Suzuki, & F. Hirose, Robust
design method of multilayer antireflection coating for organic solar cells,
IEICE, E96-C, 604-611, 2013).
Examples of other studies:
(1)FDTD method for the devices with glass substrate and its application
to the optimization of moth eye structure
S. Kubota, K. Kanomata, B. Ahmmad, J. Mizuno, & F. Hirose, Optimized
design of moth eye antireflection structure for organic photovoltaics,
J Coat Technol Res, 13: 201-210, 2016.
S. Kubota, K. Kanomata, B. Ahmmad, J. Mizuno, & F. Hirose, FDTD analysis
for light passing through glass substrate and its application to organic
photovoltaics with moth eye antireflection coating, J Photopolym Sci Technol, 29: 209-214, 2016.
(2)Design and experiment of the OPV devices integrating nanotexture and
high-refractive index glass
S. Kubota, Y. Harada, T. Sudo, K. Kanomata, B. Ahmmad, J. Mizuno, & F. Hirose, An integrated antireflection design using nanotexture and high-refractive-index glass for organic photovoltaics, J Coat Technol Res, 14: 1209-1224, 2017.
(3)Antireflection design for indoor solar cells
S. Kubota, B. Ahmmad, and F. Hirose, Optical design of multilayer antireflection
coatings for indoor solar cell applications, Applied Optics, 62: 2117-2123, 2023. |
|